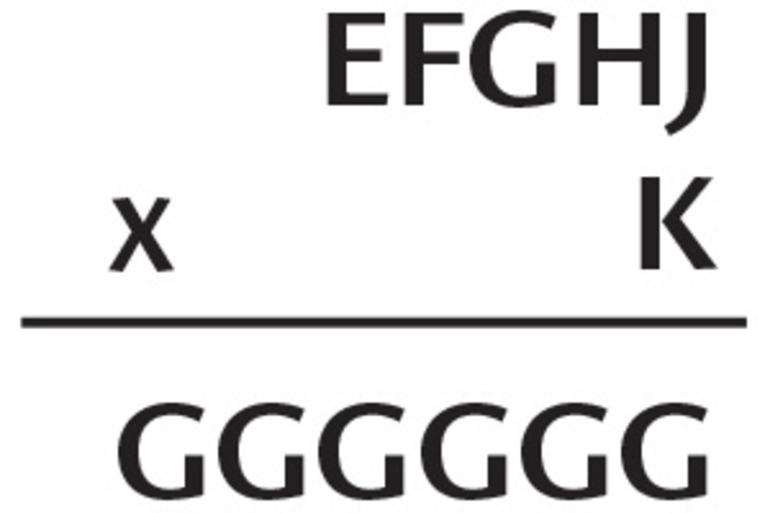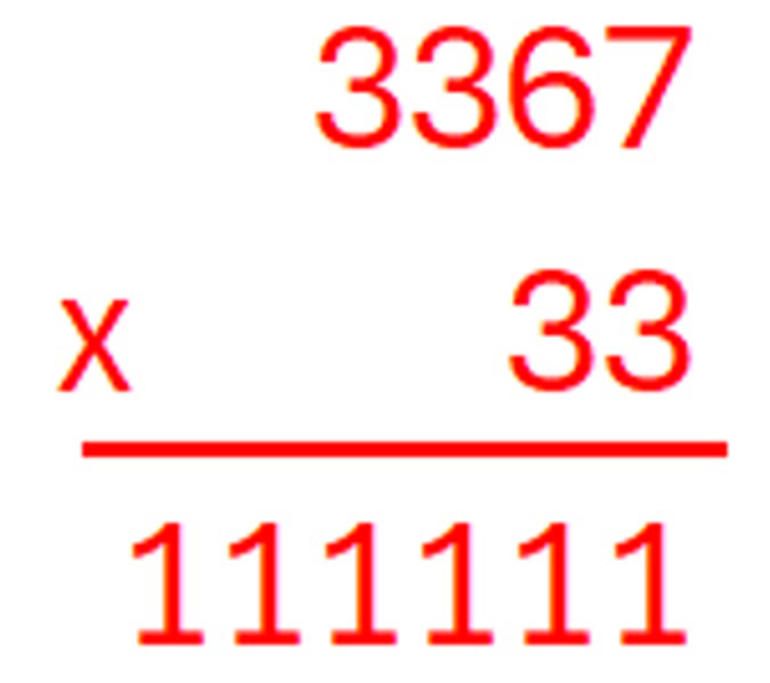MicroStockHub/iStock
Zeka Oyunları Kasım 2024 Soruları
Piyonlu Doğrular
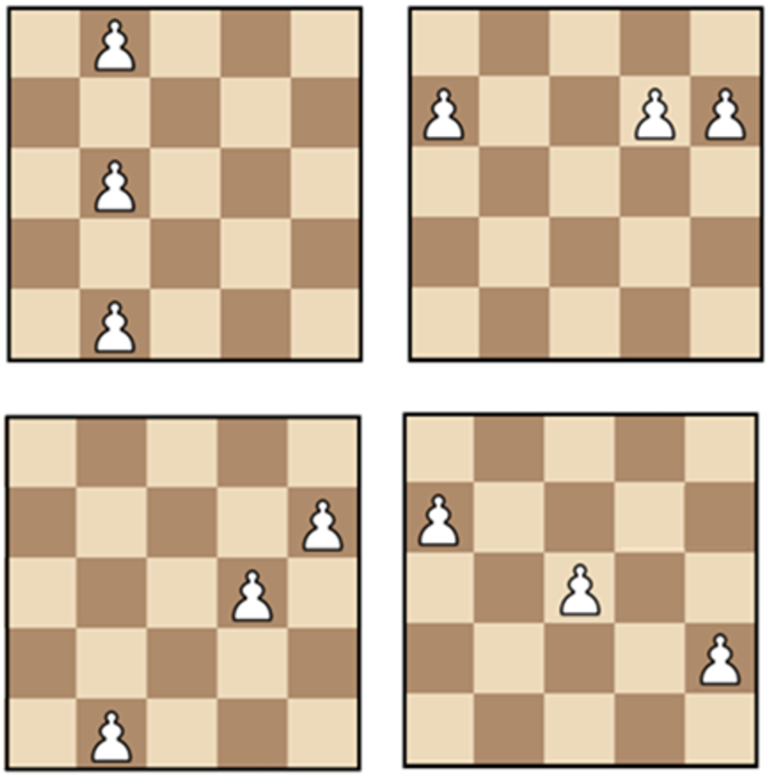
X adet piyon rastgele biçimde 5x5'lik bir satranç tahtasına yerleştirilecek. Amaç üç piyonun bulunduğu satır, sütun ya da çapraz hat üzerinde bir doğru elde etmek. Bu işi başarmayı garantilemek için X en az kaç olabilir?
Üç piyon bulunan doğru örnekleri:
Ortadaki Sayı
Dokuz farklı rakam kullanarak üç adet üç basamaklı sayı oluşturuluyor ve büyüklüklerine göre sıraya konuyor. Bu üç sayının toplamı 1999 olduğuna göre ortadaki sayı en az kaç olabilir?
Sıralı Toplamalar
Sıralamaları K<L<M<N olan dört sayı ikişerli grup halinde bir araya getirilmiş ve toplamları alınmıştır. Elde edilen 6 sayının ardışık olduğu görülmüştür. En küçük toplam 4 olduğuna göre bu dört sayının en küçüğü en fazla kaç olabilir?
Rakamlar
Üç basamaklı bir sayıdan üç basamaklı bir sayı çıkarılıyor ve üç basamaklı bir sayı elde ediliyor. Bu işlem incelendiğinde dokuz rakamın da birbirinden farklı olduğu görülüyor. Çıkarma işlemi yapılan bu iki sayının farkı 234 olduğuna göre toplamları en fazla kaç olabilir?
Çarpma
Bu çarpma işleminde her harf farklı bir rakama karşılık gelmektedir. İşlemi gerçekleştiren rakamları bulunuz.
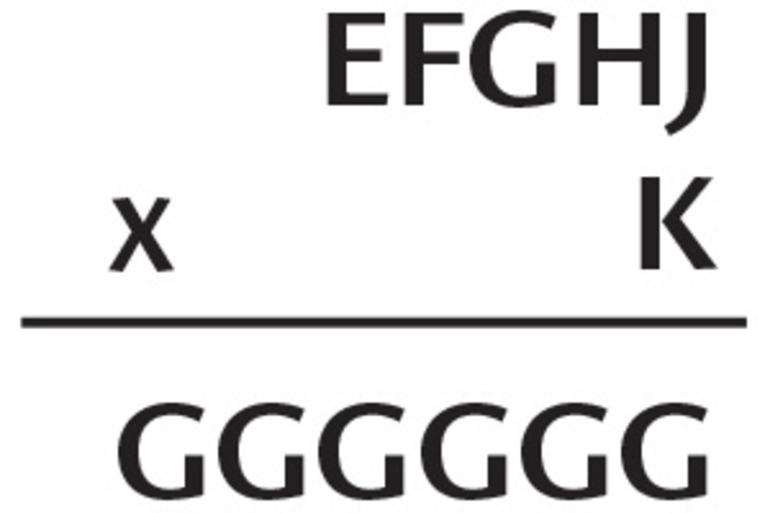
Hangisi Farklı?
Farklı olan şekli bulunuz.

Koni Bardak
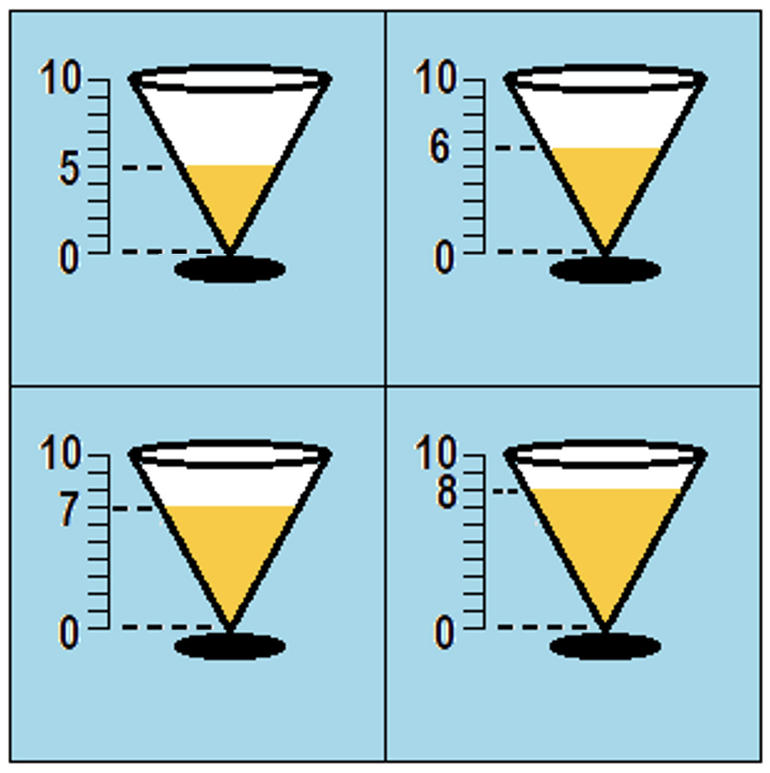
Çeşitli miktarlardaki meyve suları bulunan koni biçimindeki bardaklar şekilde görülmektedir. Aşağıdaki seçeneklerden hangisi bir bardağın tamamını doldurmaya en yakındır? (Az miktarda eksik kalabilir ya da taşabilir.)
A) I+IV
B) II+III
C) II+IV
D) III+III
E) IV+IV
Noktalar
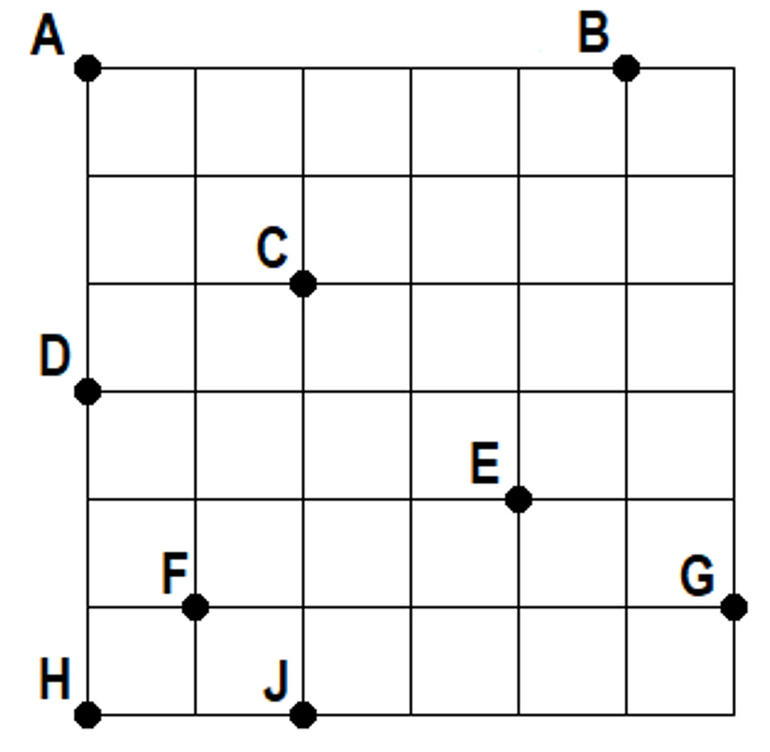
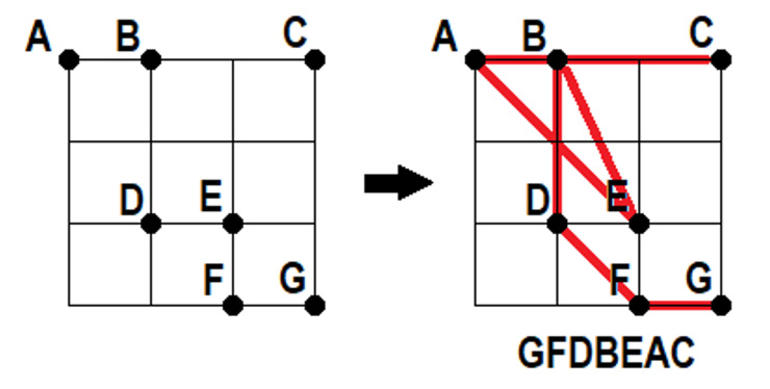
Bir noktadan başlayıp sırayla tüm noktalardan geçen ve son noktada tamamlanan bir yol oluşturacaksınız. Koşulumuz yol üzerindeki her nokta çifti arasındaki uzaklığın bir sonraki nokta çiftinin uzaklığından daha küçük olması (yani birinci nokta ile ikinci nokta arasındaki uzaklık, ikinci nokta ile üçüncü nokta arasındaki uzaklıktan daha küçük olacak ve bu durum aynı biçimde devam edecek). Not: Yolu oluşturan doğrular örnekteki gibi noktaların üzerinden geçebilir. Örnek: Soru aşağıdaki tablo için sorulsaydı çözüm sağdaki gibi olacaktı ve cevap olarak GFDBEAC girilecekti.
99 Kart
Bir kutuda 1’den 99’a kadar sayıların yazıldığı 99 kart bulunuyor. Bu kutudan rastgele kartlar çekeceksiniz. Amacınız birbirini takip eden 5 sayı elde etmek. Amacınıza ulaşmayı garanti etmek için en az kaç kart seçmeniz gerekir?
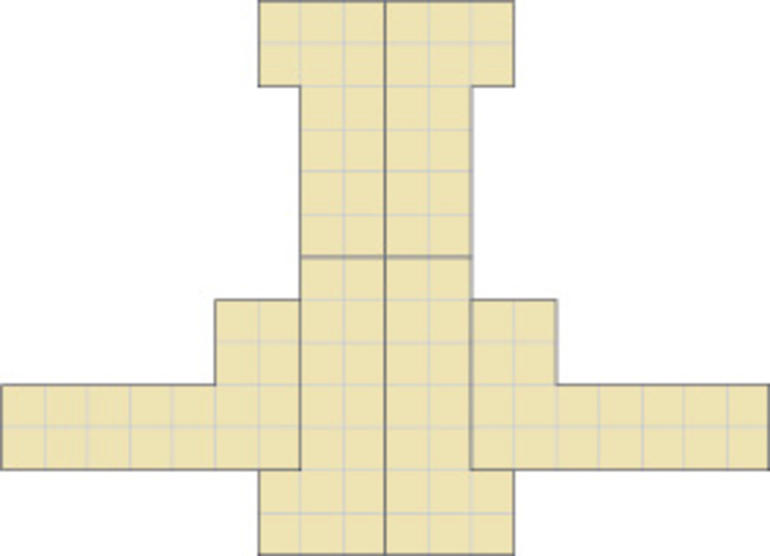
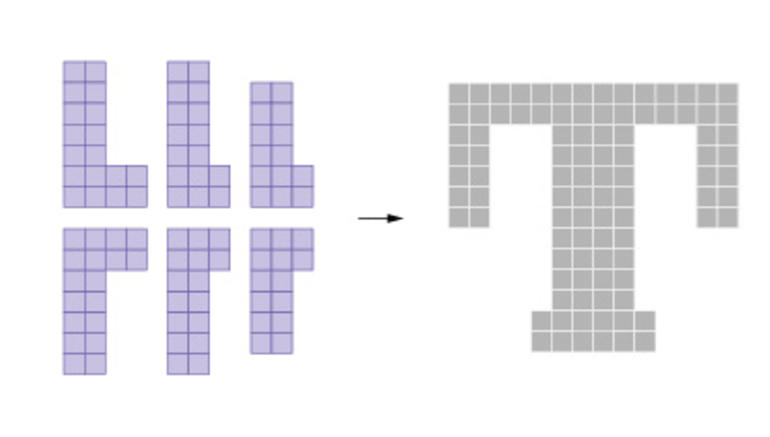
Altı “L”
Altı “L” parçasını bir araya getirerek sağdaki şekli elde ediniz. Parçalar döndürülebilir ve ters çevrilebilir.
Zekâ Oyunları Ekim 2024 Çözümleri
Piyonlar
10 piyon gerekir. Aralarındaki mesafenin en az 2 birim olduğu 9 piyonun yerleşimi şekilde görülmektedir. Onuncu piyon nereye yerleştirilirse yerleştirilsin başka bir piyonla arasındaki mesafe 2 birimden az olacaktır.

Çocuk Sayıları
Çocuk sayıları: 1, 1, 2, 4
1+1+2+4=8
1x1x2x4=8
Çarpma
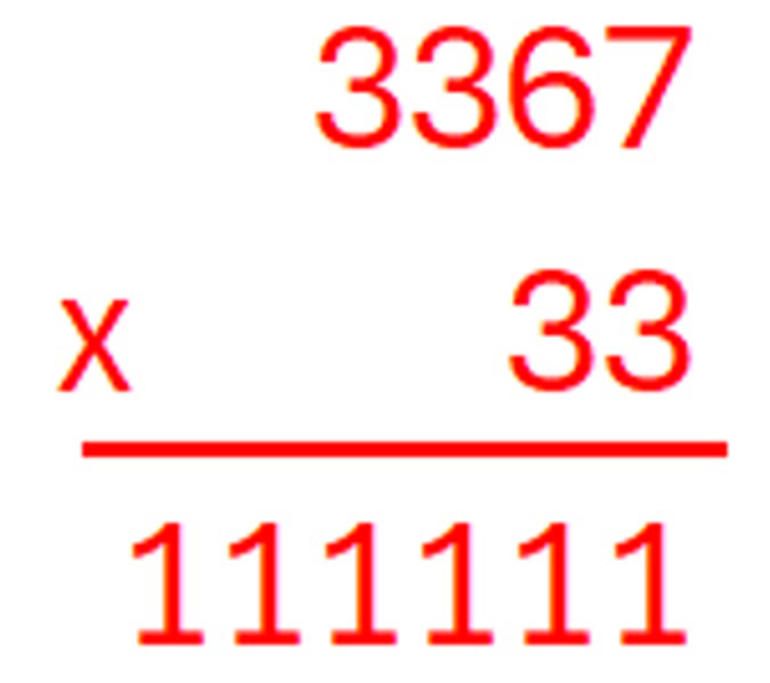
Ne Yazıyor?
ÇEKİRGE
ÜÇGEN’in ikinci harfi Ç
BEŞGEN’in ikinci harfi E
KARE’nin birinci harfi K
DAİRE’nin üçüncü harfi İ
KARE’nin üçüncü harfi R
ÜÇGEN’in üçüncü harfi G
BEŞGEN’İn ikinci harfi E
Yirmi Sayı
X en fazla 11 olabilir.
Seçilecek sayılar:
11,12,13,14,15,16,17,18,19,20,21
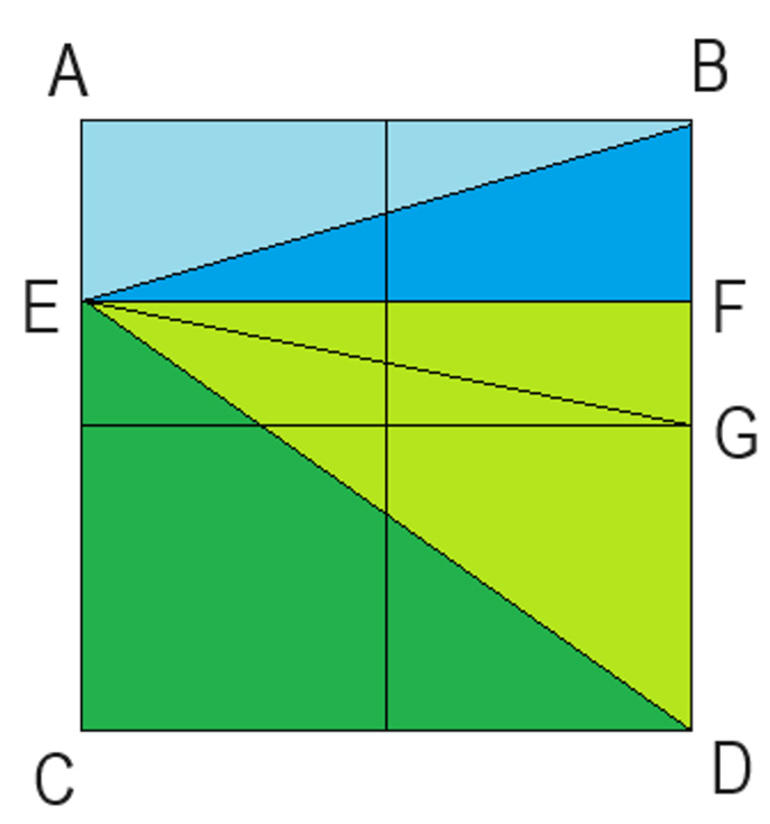
Sarı Bölge
1 birim kare.
AB ve CD doğrularına paralel EF doğrusunu çizelim.
(ABE)=(BEF) ve (CDE)=(DEF) olduğu için
(BDE)=(ABCD)/2=2
G noktası BD doğrusunun orta noktası olduğu için
(DEG)=(BDE)/2=2/2=1 birim kare.
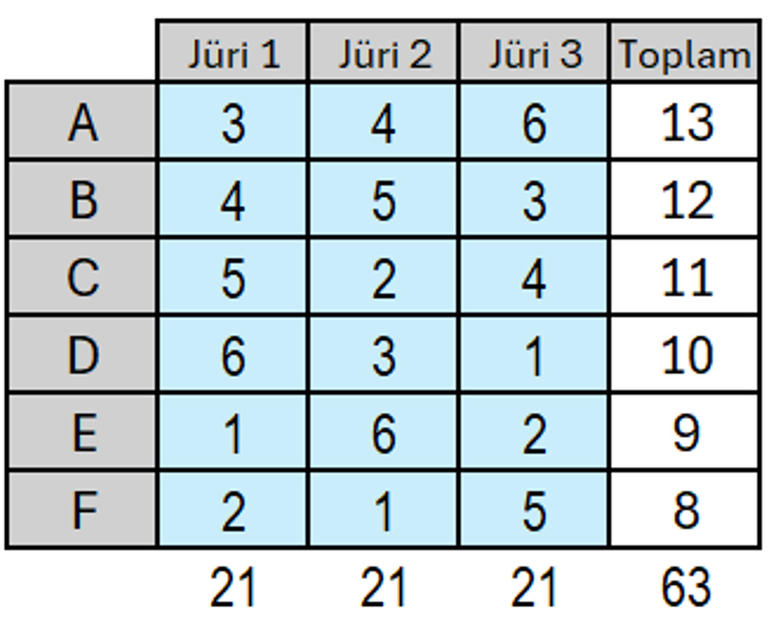
Yarışma
En yüksek toplam puanı alan yarışmacının toplam puanı en az 13 olabilir.
Örnek bir puan tablosu:
Altmış Altı Sayı
8’den başlamanız gerekir.
Soru İşareti
E gelecek.
Üçüncü sütunda diğer iki sütundaki kırmızı karelerin toplamı kadar kırmızı kare bulunuyor ve en üst satırdaki üç kare kırmızı oluyor.

ALTI "L"