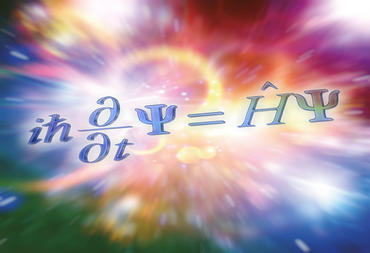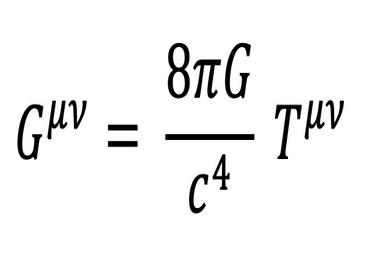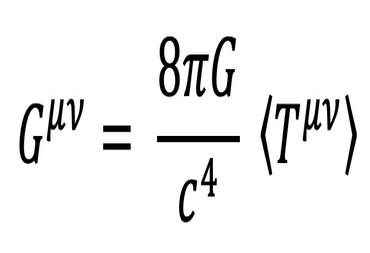chal/iStock
Kuantum mekaniği ile genel görelilik arasındaki uyumsuzluğu giderme çabalarının çoğu genel göreliliğin yerini alacak bir kuantum kütleçekimi kuramı geliştirmeye odaklanıyor. Ancak kütleçekimi, kuantum fiziğiyle açıklanamayacak bir olgu da olabilir. University College London’dan Jonathan Oppenheim, genel görelilik ile kuantum alan teorilerini bir araya getiren bir kuram geliştirdi. Oppenheim, kuramı tutarlı hale getirmek için klasik kütleçekimi ile kuantum madde arasındaki bağlantının tersinir olmadığını varsaydı. Thomas Galley, Flamina Giacomini ve John Selby tarafından yapılan kuramsal çalışmalar da klasik kütleçekimi ile kuantum maddeyi bir araya getirebilecek herhangi bir tutarlı kuramın hem klasik fiziğin hem de kuantum fiziğinin temel bir özelliği olan tersinirliği içermemesi gerektiğini gösteriyor.
Genel Görelilik Kuramı Nedir?

Richard Jones/Science Photo Library
Genel görelilik kuramı dört temel etkileşimden biri olan kütleçekimini açıklar. Albert Einstein tarafından yüz yıldan uzun bir süre önce geliştirilen bu klasik kuram, kütleçekimini uzayzamanın geometrisiyle ilişkilendirir: Kütle uzayzamanı büker, kütlenin uzayzamandaki hareketleri ise uzayın eğriliği tarafından yönlendirilir. Genel görelilik kuramı uzayzamanın geometrisinin, içerisindeki kütleler tarafından belirlendiğini söyler.
Genel görelilik kuramı, Isaac Newton’un 1600’lerde geliştirdiği, iki madde parçasının birbirlerine kütleleriyle doğru orantılı, aralarındaki mesafenin karesiyle ters orantılı bir çekim kuvveti uyguladığını öne süren kütleçekim kuramının açıklayamadığı pek çok olguyu başarıyla açıklar. Bugüne kadar çok sayıda testten başarıyla geçti ve elimizdeki en iyi kütleçekimi kuramı olmaya devam ediyor.

Mark Garlick/Science Photo Library
Kuantum Fiziği Nedir?
1800’lerin sonlarında klasik fiziğin çeşitli olguları açıklamakta başarısız olduğu anlaşılmıştı. Örneğin, atomların yapısı ya da kara cisim ışıması ile ilgili veriler klasik fizikle açıklanamıyordu. Kuantum fiziğinin geliştirilmesi bu sorunlara bir çözüm getirdi.
Kuantum fiziğini klasik fizikten ayıran temel özelliklerden biri süreksizliktir. Örneğin, klasik fiziğe göre, belirli bir frekanslı bir ışık ışınının enerjisi herhangi bir değeri alabilir. Kuantum fiziği ise ışık ışınlarının içinde foton olarak adlandırılan enerji paketleri olduğunu söyler. Belirli bir frekanslı bir ışık ışınının enerjisi ancak içerdiği fotonların enerjisinin tam katı olabilir. Atomlardaki enerji seviyeleri de kuantum fiziğindeki süreksizliğin (kuantizasyonun) bir başka örneğidir.
Kuantum fiziğinin klasik fizikten bir diğer farkı belirsizliklerdir. Klasik fizikte bir sistemin tüm özelliklerinin ufak hata paylarıyla belirlenebilmesi mümkündür. Werner Heisenberg tarafından formüle edilen belirsizlik ilkesi ise bir sistem hakkında edinilebilecek bilgilerin bir sınırı olduğunu ifade eder. Belirli özellik çiftlerinden (örneğin, konum ve momentum) biri hakkında ne kadar iyi bilgi sahibiysek diğeri hakkındaki bilgimiz o kadar azdır.
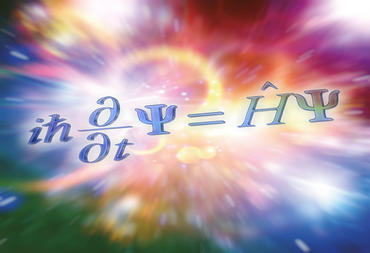
Kuantum mekaniğinde bir sistemin özellikleri hakkında tahminler yapmak için Schrödinger denkleminden yararlanılır. Schrödinger denkleminin çözümleri, dalga fonksiyonu olarak adlandırılır. Dalga fonksiyonu ise sistem üzerinde yapılacak ölçümlerin muhtemel sonuçlarının hangi olasılıklarla ortaya çıkacağı hakkında bilgi verir.
Alfred Pasieka / Science Photo Library
Schrödinger dalga denklemi
Kuantum fiziğinin, günlük hayatta aşina olmadığımız en sıra dışı özelliklerinden biri süperpozisyondur. Bir parçacığın spin açısal momentumunun (kısaca spininin) ölçüleceğini düşünelim. Muhtemel iki sonuç vardır: Parçacığın spini ya ölçüm yapılan yönde ya da bu yönün zıddındadır. Böyle bir parçacığın dalga fonksiyonu ölçümden önce bu iki durumdan herhangi birinde olabileceği gibi, bu iki durumun bir süperpozisyonunda (lineer kombinasyonunda) da olabilir. Bu durumda ölçüm sonucunun ne olacağı hakkında ancak olasılık hesapları yapılabilir. Örneğin, dalga fonksiyonu kullanılarak yapılan hesaplar, spininin %60 olasılıkla bir yönde, %40 olasılıkla diğer yönde bulunacağı sonucunu verebilir. Bu durumda yüz özdeş parçacık üzerinde aynı ölçüm yapılırsa kuramsal tahminlerle uyumlu bir biçimde 60’ının spininin bir yönde, 40’ının da diğer yönde olduğu bulunur.
Günümüzde kuantum mekaniği hakkındaki kuramsal tartışmalara en çok konu olan şeylerden biri ölçümlerdir. Kuantum fiziğinin en yaygın kabul gören yorumu olan Kopenhag yorumu, ölçüm sonucunda, dalga fonksiyonunun, bulunan sonuca karşılık gelen kuantum durumuna “çöktüğünü” söyler. Bu durum, ölçümlerin süperpozisyon durumlarını yok ederek sistemin klasikleşmesine neden olduğu anlamına gelir. Ölçüm sonuçları olasılığa dayalı olduğu için ölçümler Schrödinger denklemi kullanılarak yapılan hesapları kesintiye uğratır. Bu durum sıklıkla ölçüm paradoksu olarak adlandırılır.
Günümüzde dört temel etkileşimden üçü (elektromanyetik, güçlü ve zayıf etkileşimler) kuantum alan kuramlarıyla açıklanıyor. Bu kuramlarda etkileşimler kuvvet taşıyıcıları olarak adlandırılan temel parçacıklar aracılığıyla gerçekleşiyor. Fotonlar elektromanyetik etkileşime, glüonlar güçlü etkileşime, W ve Z bozonları da zayıf etkileşime aracılık ediyor.
Genel Görelilik ile Kuantum Fiziğinin Uyumsuzluğu
Genel görelilik klasik bir kuramdır ve dolayısıyla kuantum fiziği ile uyumlu değildir. Bu durumu görmek için Einstein alan denklemlerine göz atmak yeterlidir:
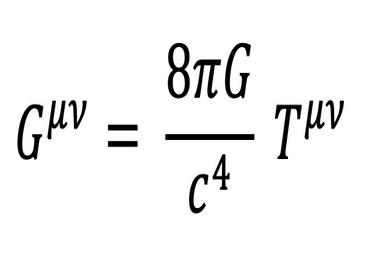
Bu eşitliğin sol tarafından uzayzamanın yapısıyla ilgili bilgilerin kodlandığı Einstein tensoru (Gµⱱ) yer alır. Eşitliğin sağ tarafında ise madde ile ilgili bilgilerin kodlandığı stres-enerji tensoru (Tµⱱ) vardır. Einstein eşitliğini kullanarak uzayzamanın yapısı hakkında hesaplar yapmak için stres-enerji tensorunun ve dolayısıyla uzaydaki madde ve enerji dağılımının ne olduğunu bilmeniz gerekir. Ancak kuantum fiziği bu bilgileri kesin olarak elde etmenin imkânsız olduğunu söyler. Kuantum fiziğindeki belirsizlikler ile klasik fiziğin kesinliği nasıl bir araya getirilebilir? Kuantum maddenin uzayzaman üzerindeki etkileri nasıl bir kuramla açıklanabilir?
Yarıklasik Kütleçekimi
Günümüzde kuantum maddenin klasik kütleçekim alanı üzerindeki etkilerini hesaba katmak için yarıklasik Einstein denklemi kullanılıyor. Yarıklasik denklemin klasik denklemden temel farkı, eşitliğin sağ tarafında klasik stres-enerji tensorunun değil stres-enerji tensorunun “beklenti değerinin” yer almasıdır:
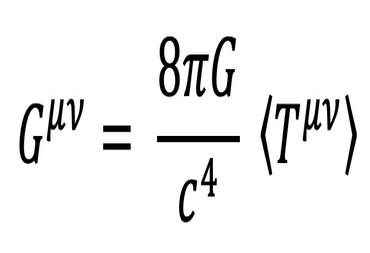
Bu denklemi kullanarak uzayzamanın geometrisini belirlemek için öncelikle kuantum mekaniksel hesaplarla stres-enerji tensorunun beklenti değerinin hesaplanması gerekir.
İlk olarak beklenti değerinin ne anlama geldiğine bir göz atalım. Bir boyutlu bir kutunun içinde momentumunun büyüklüğü p olan bir parçacık olsun. Parçacık, kutunun içinde durmaksızın hareket etmekte, kutunun duvarlarına çarptıkça esnek bir biçimde (enerji kaybetmeksizin) geri yansımaktadır. Parçacık belirli bir anda kutunun içinde ya bir yöne ya da diğer yöne doğru hareket ettiği ve momentumunun büyüklüğü p olduğu için parçacığın momentumu üzerinde yapılacak bir ölçüm %50 olasılıkla +p, %50 olasılıkla da -p sonucunu verecektir. Bu durumda momentumun beklenti değerini (50*(+p) + 50 * (-p)) / 100 = 0 olarak hesaplarız. Bu değer, özdeş sistemler üzerinde tekrar tekrar yapılacak ölçümlerin, ölçüm sayısı sonsuza giderken, vereceği sonuçların ortalamasına karşılık gelir. Parçacığın belirli bir andaki momentumun ne olduğu belirsiz olsa da momentumunun beklenti değeri belirli bir sayıdır. Benzer biçimde, her ne kadar kuantum maddenin konumunda ve enerjisinde belirsizlikler olsa da stres-enerji tensorunun beklenti değerinin ne olduğu belirlidir. Dolayısıyla yarıklasik alan denklemi kuantum madde içeren sistemlerde, klasik hesaplarla, uzayzamanın yapısının belirlenmesine imkân verir. Peki, yarıklasik alan denklemi ne ölçüde doğrudur?
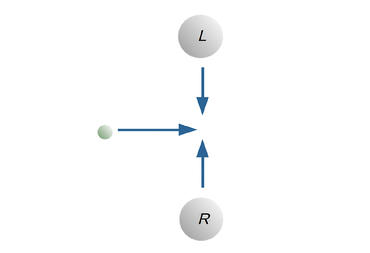
Kütleli bir cismin iki ayrı konumun iki ayrı konumun bir süperpozisyonunda olduğunu düşünelim. Bu konumlardan biri a noktası, diğeri b noktası olsun. Bu durumda parçacığın “beklenen konumu” a ve b noktalarının ortalarında bir yerlerde olacaktır. Dolayısıyla eğer yarıklasik alan denklemi doğruysa, böyle bir parçacığın etrafındaki nesneleri a noktasına ya da b noktasına doğru değil, bu iki noktanın arasında bir yerlere doğru çekmesi ve hatta kendisinin de bu noktaya doğru ivmelenmesi beklenir.
Yarıklasik Einstein alan denklemine göre L ve R noktalarının süperpozisyonundaki bir gezegenin bu iki noktanın ortalarında bir yerlere doğru bir çekim alanı oluşturması gerekir. Ancak deneyler bu tahmini doğrulamıyor.
Geçmişte bu tahmini test etmek için yapılan deneylerse olumlu sonuç vermedi. Yarıklasik Einstein alan denklemi, belirsizliklerin görece ufak olduğu durumlar için iyi bir yaklaşım sağlasa da kütleçekiminin doğru bir betimlemesini yapmıyor. Yarıklasik kuramla deneyler arasındaki bu uyumsuzluk genel olarak kütleçekiminin klasik bir olgu olmadığına dair bir kanıt olarak görülüyor.
Kuantum Kütleçekim Kuramları
Günümüzde fizikçiler arasındaki yaygın kanı, kuantum maddenin uzayzaman üzerindeki etkilerini açıklayan, genel göreliliğin yerini alacak bir kuantum kütleçekimi kuramının geliştirilmesi gerektiği. Sonuçta, dört temel etkileşimin üçü kuantum kuramlarıyla açıklanıyor. Neden kütleçekimi de diğer etkileşimler gibi kuantum fiziğiyle açıklanabilecek bir olgu olmasın?
Bir kuantum kütleçekimi kuramının bugün paradoks olarak görülen çeşitli kuramsal sorunlara da bir çözüm getireceği düşünülüyor. Örneğin, genel görelilik bir karadeliğe düşen cismin karadeliğin merkezindeki tekillikte yok olacağını, kuantum mekaniği ise karadeliklerin kütleleriyle ters orantılı bir sıcaklığa sahip olduğunu ve ışıma yapacağını söyler. Ancak kuramsal olarak karadeliklerin yaptığı ışıma istatistiksel dağılım gösterir, dolayısıyla karadeliklerin etrafında yaydığı ışımayı gözlemleyerek geçmişte karadeliğe düşmüş maddeler hakkında bilgi edinilemez. Bu durum bir paradoks olarak görülür, çünkü bilginin korunumu modern fiziğin temel ilkelerinden biridir. Karadelik-bilgi paradoksunun çözümünün ancak bir kuantum kütleçekimi kuramının geliştirilmesiyle mümkün olacağı düşünülüyor.

Victor de Schwanberg/Science Photo Library
Stephan Hawking’in karadeliklerin ışıma yaptığını gösteren çalışmaları kuramsal fizikte karadelik-bilgi paradoksu olarak anılan bir paradoksa yol açtı.
Günümüzde doğru bir kuantum kütleçekimi kuramı olmaya aday çeşitli kuramlar var. Örneğin sicim teorisi, klasik fizikte noktasal (boyutsuz) olarak düşünülen temel parçacıkları sicimler olarak ele alıyor. Kuramın tahminleri arasında, kütleçekimine aracılık ettiği düşünülen bir kuvvet parçacığı (graviton) da var. Halka kuantum kütleçekimi kuramı ise uzayın da kuantize olduğunu, maddenin atomlardan meydana gelmesine benzer biçimde uzayın da ufak birimlerin bir araya gelmesiyle oluştuğunu öne sürüyor.

Spencer Sutton/Science Photo Library
Bir kuantum kütleçekimi kuramının geliştirilmesinin gerekliliği fizikçiler arasında yaygın kanı olsa da bugüne kadar hiçbir kuantum kütleçekimi kuramı gözlemlerle ve deneylerle doğrulanabilmiş değil. Hatta kütleçekiminin kuantum mekaniksel bir olgu olup olmadığı bile hâlâ tartışma konusu.
Klasik Kütleçekimi ile Kuantum Mekaniğini Bir Araya Getirmek Mümkün mü?

Mark Garlick / Science Photo Library
Bugün pek çok fizikçinin bir kuantum kütleçekimi kuramı geliştirmeye çalışmasının nedenlerinden biri de yıllar içinde klasik kütleçekimi ile kuantum fiziğini bir araya getirmenin imkânsızlığına dair çeşitli düşünce deneyleri ve hatta teoremler öne sürülmüş olması. Bu düşünce deneyleri ve teoremler, kütleçekiminin klasik bir olgu olması durumunda, belirsizlik ilkesinin ihlal edilmesi ya da ışıktan hızlı bilgi aktarılması gibi, temel fizik bilgileriyle çelişkili sonuçlar ortaya çıkacağını gösteriyor.
Klasik kütleçekimi ile kuantum fiziğini bir araya getirmenin imkânsızlığına dair düşünce deneylerinden biri, Richard Feynman tarafından öne sürülmüştü. Feynman’ın düşünce deneyi özetle şöyle ilerler: Kuantum mekaniği ilkelerine uygun davranan kütleli bir parçacık, bir çift yarığın üzerine gönderilir. Kuantum mekaniği böyle bir durumda parçacığın bir dalga gibi davranacağını ve yarıkların arkasındaki bir detektörde girişim desenleri ortaya çıkacağını söyler. Parçacığın hangi yarıktan geçtiğini belirlemek amacıyla yapılacak herhangi bir ölçümse, parçacığın davranışlarının klasikleşmesine ve girişim deseninin yok olmasına yol açacaktır. Feynman, deney sırasında ortamdaki kütleçekim alanının ölçülmesini önerir.
Eğer kütleçekimi klasik fizikle açıklanacak bir olguysa, parçacığa herhangi bir müdahalede bulunmadan, parçacığın hangi yarıktan geçtiğini tespit etmek mümkün olacaktır. Bu durum kuantum mekaniği ilkeleri açısından bir çelişki ortaya çıkarır: Parçacığın kuantum durumu üzerinde bir ölçüm yapılmadığına göre, parçacık dalga gibi davranmalı ve ortaya bir girişim deseni çıkmalıdır. Diğer taraftan, kütleçekim alanını ölçerek parçacığın hangi yarıktan geçtiği kesin olarak tespit edilebileceği için parçacığın davranışları klasikleşmeli ve girişim deseni yok olmalıdır.
Hem Feynman’ın düşünce deneyinde hem de kütleçekiminin kuantum mekaniksel bir olgu olduğunu ispatlamak için öne sürülmüş diğer düşünce deneylerinde ve teoremlerde esasen gizli bir varsayım var. Feynman, kütleçekiminin klasik bir kuramla açıklanabilmesinin, kuantum fiziğinin deneylerle defalarca kez doğrulanmış ilkeleriyle çelişeceğini öne sürerken, kuantum madde ile kütleçekim alanı arasındaki ilişkinin determinist olduğunu varsayıyor.
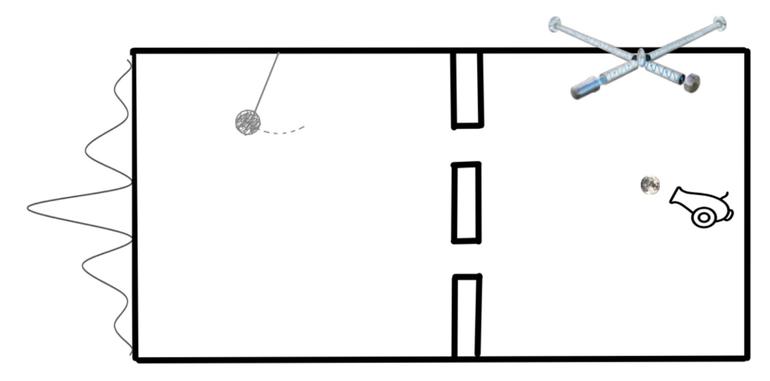
Feynman’ın düşünce deneyinin bir betimlemesi
Etkileşimin determinist olması zamanda ileriye ya da geriye dönük kesin tahminler yapılabileceği anlamına gelir. Örneğin, klasik mekanikteki hareket denklemleri deterministtir. Bir parçacığın belirli bir andaki konumunu ve hızını biliyorsanız, hareket denklemlerini kullanarak gelecekteki ya da geçmişteki herhangi bir zamanda konumunun ve hızının ne olduğu kesin olarak hesaplanabilir. Her ne kadar kuantum fiziği olasılığa dayalı bir teori olsa da kuantum fiziğinin temeli olan Schrödinger denklemi de deterministtir. Bir sistemin belirli bir andaki dalga fonksiyonunun ne olduğunu biliyorsanız, Schrödinger denklemini kullanarak gelecekte ya da geçmişte herhangi bir andaki dalga fonksiyonunu düşünce deneyindeki argümanı geçersiz kılar. Çünkü Feynman düşünce deneyinde, kütleçekim alanı ölçümleri yapılarak parçacığın takip ettiği rotanın kesin olarak belirlenebileceğini varsayıyor. Kütleçekiminin klasik bir olgu olamayacağını öne süren teoremler için de aynı durum söz konusu.

Mark Garlick/Science Photo Library
Stokastik Kuramlar ve Tersinirlik
Determinist kuramlarla stokastik kuramlar arasındaki temelbir fark tersinirlik ile ilgilidir. Bir sistemin belirli bir andaki durumunu ele alıp, belirli bir süre için geleceğe dönük determinist hesaplar yaptığınızı düşününün. Bulduğunuz sonucu alıp aynı hesapları, aynı süre için ters yönde (zamanda geriye doğru) yaptığınızda bulacağınız sonuç, başlangıçtaki durum olacaktır. Çünkü kuramın açıkladığı etkileşimler determinist bir biçimde gerçekleşmektedir. Aynı durum stokastik kuramlar için geçerli değildir. Bir sistemin belirli bir andaki durumunu alıp geleceğe dönük olasılığa dayalı hesaplar yapar, daha sonra bulduğunuz sonucu alıp aynı hesabı ters yönde yaparsanız sonucun başlangıçtaki durumun aynısı olması olasılık dışıdır. Stokastik kuramlarda tersinirlik özelliği yoktur.
Kütleçekimi ile Kuantum Maddeyi Bir Araya Getirmenin Alternatif Yolları

Victor de Schwanberg/Science Photo Library
Kütleçekimi ile kuantum fiziği ilkelerine uygun davranan maddeyi bir araya getirmenin alternatif yolları neler olabilir? Bu soruya cevap veren bir çalışma yakın zamanlarda Thomas Galley, Flamina Giacomini ve John Selby tarafından yapıldı. Araştırmacıların Quantum’da yayımladıkları makalelerinde ispatladıkları teoremlerden biri şöyle: G ve S olarak adlandıracağımız iki sistem ve bu sistemler arasında bir I etkileşimi olsun. Bu durumda şu dört varsayımın tamamı doğru olamaz:
- S sistemi klasik değildir,
- I etkileşimi tersinirdir,
- S sisteminden G sistemine bilgi akışı vardır,
- G sistemi klasiktir.
Bu teoremi kuantum madde ve kütleçekimine uyguladığımızı düşünelim. G sistemi kütleçekim alanı, S sistemi de atomlar, moleküller gibi kuantum mekaniği ilkelerine uygun davranan parçacıklardan oluşan bir sistem olsun. Bu durumda aynı anda doğru olamayacak dört varsayım şu şekilde ifade edilebilir:
- Kuantum maddeden oluşan sistem klasik değildir,
- I etkileşimi tersinirdir,
- Kuantum maddeden kütleçekim alanına bilgi akışı vardır,
- Kütleçekim alanı klasiktir.
Bu dört varsayımın hangisi ya da hangilerinden vazgeçilebilir? İlk varsayımdan vazgeçilemeyeceği açık. Kuantum fiziği zaten atomlar ve moleküller gibi parçacıkların davranışlarının klasik fizikle açıklanamaması üzerine geliştirilmiştir. Üçüncü varsayımdan vazgeçilmesi de olası gözükmüyor. Kuantum maddeden kütleçekim alanına bilgi akışı olmaması, kütleçekim alanının kuantum maddeden etkilenmediği anlamına gelir. Ancak kuantum madde de kütle taşır. Dolayısıyla kütleçekim alanı kuantum madde tarafından da belirlenmelidir.
Geriye iki varsayım kalıyor. Eğer kütleçekim alanının klasik olduğu varsayımını doğru kabul etmeye devam edersek, bu durumda kuantum madde ile kütleçekim alanı arasındaki etkileşimin tersinir olduğu varsayımından vazgeçilmesi gerekiyor. Eğer kütleçekim alanının klasik olduğu varsayımı yanlış kabul edilirse, bu durumda ikinci varsayım (etkileşimin tersinir olduğu varsayımı) doğru ya da yanlış olabilir.
Kısacası Galley, Giacomini ve Selby’nin teoremi, kuantum madde ile kütleçekimini bir araya getirmenin iki alternatif yolu olduğunu gösteriyor. Bu alternatiflerden biri, bugün pek çok kuramsal fizikçinin üzerine çalıştığı gibi, bir kuantum kütleçekimi kuramı geliştirmek. Şayet ikinci alternatifi seçiyor ve kütleçekiminin klasik bir olgu olduğunu varsayıyorsanız, bu durumda geliştireceğiniz kuramda tersinirlik özelliğinin olmaması gerekiyor. Hangi alternatifin sizi doğru sonuca ulaştıracağını ise ancak deneyler ve gözlemler söyleyebilir.
Postkuantum Klasik Kütleçekimi

Mark Garlick/Science Photo Library
University College London’dan Jonathan Oppenheim Physical Review X’te yayımladığı bir makalede genel görelilik ile kuantum alan teorisini tutarlı bir biçimde bir araya getiren bir kuram geliştirmeyi başardığını açıkladı. Oppenheim’ın kuramında genel görelilik ve kauntum fiziği kendi doğasını koruyor. Kuantum madde ile kütleçekim alanı arasındaki eşleşme ise stokastik bir biçimde gerçekleşiyor. Dolayısıyla kuramda tersinirlik özelliği yok. Oppenheim’ın kuramı, postkuantum teorileri olarak adlandırılan kuantum durumları ya da uzayla ilgili dinamik denklemlerin modifiye edildiği kuramların bir örneği.
Oppenheim çalışmasına ilk olarak bir klasik ve bir kuantum sistemin bir araya gelmesi durumunda sistemin durumunun nasıl tanımlanacağını ele alarak başlıyor. Oppenheim’ın kuramında sistemin klasik ve kuantum tarafları için ayrı ayrı istatistiksel yaklaşımlar kullanılıyor.
Kuantum mekaniksel sistemin durumu yoğunluk operatörü diye adlandırılan açık (çevreden kontrolsüz müdahalelere maruz) kuantum sistemlerinin durumunu tanımlamak için kullanılan bir operatörle tanımlanıyor. Klasik sistemin durumunu tanımlamak içinse olasılık dağılımları (çok sayıda parçacık içeren ve içerdiği parçacıkların tek tek konumlarının bilinmediği sistemler için kullanılan bir yöntem) kullanılıyor. Oppenheim bu iki istatistiksel yaklaşımdan yararlanarak bir “klasik kuantum durumu” tanımlıyor. Klasik kuantum durumu sistem hakkında şöyle bilgiler veriyor: Bir parçacık %20 ihtimalle uzayın belirli bir bölgesinin içindedir ve parçacığın spin durumu iki muhtemel ölçüm sonucunun belirli bir süperpozisyonundadır.

Richard Jones/Science Photo Library
Oppenheim klasik kuantum durumun tanımını yaptıktan sonra klasik sistem ile kuantum sistem arasındaki etkileşimleri tanımlayan genel bir kuram geliştiriyor. Yeni kuramda sistemin klasik ve kuantum parçaları kendi doğasını koruyor. Örneğin, kuantum sistemde belirsizlik ilkesi geçerli kalmaya devam ediyor, klasik sistemde ise ışıktan daha hızlı bilgi aktarımı gerçekleşmiyor. Sistemin iki parçası arasındaki etkileşim ise stokastik bir biçimde gerçekleşiyor. Bu durum kuramın bütününde tersinirlik özelliğinin olmamasına yol açıyor. Ancak kuramın, kuantum ve klasik alt sistemlerin kendi içindeki gelişimini tanımlayan kısımları tersinirlik özelliğini korumaya devam ediyor.
Oppenheim’ın kuramı ölçüm paradoksuna da bir çözüm getiriyor. Yeni kuramda, kuantum sistemin durumu ölçüm sonucunda anlık olarak çökmüyor, sistemin iki parçası arasındaki etkileşimler kuantum sistemin doğal olarak klasikleşmesine yol açıyor. Kuramda sistemin farklı durumları arasında olasılığa dayalı sıçramalar gerçekleşiyor ki, bu sıçramalar sistem üzerinde yapılan ölçümlerin sonuçlarına karşılık gelebilir.
Oppenheim, bir sonraki aşamada genel kuramı kütleçekim alanı ile kuantum maddeyi bir araya getiren bir teori geliştirmek için kullanıyor. Ortaya çıkan hibrit kuram, kuantum alanların stokastik bir biçimde uzayzamanın dokusunu değiştirmesine de izin veriyor. Teori, klasik limitte genel görelilik kuramına indirgeniyor. Kütleçekiminin klasik olduğunun varsayılması kuantum mekaniğinin dinamik yasalarında değişimlere yol açıyor. Oppenheim’ın kuramı karadelik-bilgi paradoksuna da sıra dışı bir çözüm sunuyor: kuramdaki stokastik etkileşimler nedeniyle bilgi korunmuyor!
Sonuç

Sakkmesterke / Science Photo Library
Jonathan Oppenheim’ın genel görelilik ile kuantum fiziğini tutarlı bir biçimde bir araya getirmeyi başaran bir postkuantum kütleçekimi kuramı geliştirmeyi başardı. Yeni kuram deneylerle ve gözlemlerle defalarca kez doğrulanmış kuramlarla uyumlu.
Geliştirilen kurama iki açıdan bakmak mümkün. Birincisi, “temel bir kuram” olarak ele alınabilir. Eğer öyleyse ve gerçekten de doğal süreçlerin doğru bir betimlemesini yapıyorsa, bu durum kütleçekiminin klasik bir olgu olduğu anlamına gelir. İkinci olarak, geliştirilen kuram, bugün ne olduğu bilinmeyen, belki de gelecekte bir gün geliştirilecek bir kuantum kütleçekimi kuramının “klasik limiti” olarak da düşünülebilir. Oppenheim’ın kuramı gelecekte deneylerle test edilebilecek çeşitli tahminler de yapıyor. Örneğin, kuramın tahminleri arasında yer alan kuantum sistemlerin kütleçekimi etkisiyle klasikleşmesi ya da farklı durumlar arasındaki sıçramalar gibi olgular, yakın gelecekte deneylerle test edilebilir.
Böylece kuramın ne ölçüde doğru olduğu hakkında daha net bir fikir edinilebilir.
Kaynaklar:
- Oppenheim, J., “A Postquantum Theory of Classical Gravity”, Physical Review X, Cilt 13, Makale No: 041040, 2023.
- Galley, T. D., “Might There Be No Quantum Gravity After All?”, Physics, Cilt 16, s. 203, 2023.
- Oppenheim, J., “Is it time to rethink quantum gravity?”, arXiv, https://arxiv.org/abs/2310.12221, 2023.
- Galley, T. D., ve ark., “Any consistent coupling between classical gravity and quantum matter is fundamentally irreversible”, Quantum, Cilt 7, s. 1142, 2023.
- Oppenheim, J., ve ark., “Gravitationally induced decoherence vs space-time diffusion: testing the quantum nature of gravity”, Nature Communications, Cilt 14, s. 7910, 2023.
- Page, D. N. ve Geilker C. D., “Indirect Evidence for Quantum Gravity”, Physical Review Letters, Cilt 47, s. 979, 1981.