Gerçi üç boyutlu bir görüntünün orijine göre simetriğini akılda canlandırmak pek kolay değil. Ancak yukarıda anlatılmaya çalışılanları açıklığa kavuşturmak için, bir aynaya başvurabiliriz. Ayna düzlemi bildiğimiz gibi, orijine göre simetrinin en basit örneğini verir ve eğer koordinat eksenlerinden birisi kendisine dikse, sadece bu koordinat ekseninin yönünü değiştirir. Aynı zamanda solu sağa, sağı da sola çevirir.

Yandaki şeklin sol tarafında, bir sağ el koordinat sistemi (x,y,z) görülüyor. Bu sistemin içinde; x eksenine paralel bir eksen etrafında, yani y-z düzlemine paralel bir düzlem üzerinde dönen ince bir disk var. Disk bir yandan dönerken, bir yandan da, x ekseni yönünde H hızıyla ilerliyor.

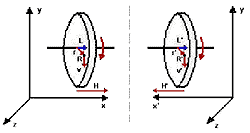
Diskin dönme yönü, sağ el kuralına göre, keza x ekseni yönünde. Dolayısıyla, mavi renkli okla gösterilmiş olan açısal momentum L'nin yönü de bu yönde seçilmiş. Ayrıca disk üzerindeki bir R noktasının, diskin merkezine göre konum vektörü r, hız vektörü ise v ile gösterilmiş. Bunlar, yani r ile v 'kutupsal vektör'ler. Ortadaki kesikli çizgi, x eksenine dik bir ayna düzlemini temsil ediyor. Şeklin sağ tarafında ise, soldaki görüntünün bu aynadaki yansıması var. Görüntüde, koordinat eksenlerinden y ile z aynı kalırken, sadece x ekseni yön değiştirmiş. Bu durum, görüntüdeki (x',y,z) koordinat sistemini sol el sistemine çevirmiş. Koordinat eksenlerinden y ile z aynı kaldığı için, y-z düzleminde yatan r ile v'nin görüntüleri, 'kutupsal vektör' olmalarına karşın, yön değiştirmemiş. Diskin yatay hız vektörü H ise, x ekseni doğrultusunda yattığı ve bir 'kutupsal vektör' olduğu için, görüntüde yön değiştirmiş. Ama x ekseni de yön değiştirdiğinden, işareti aynı kalmış. Halbuki açısal momentum vektörü L; x ekseni doğrultusunda yatmasına karşın ve fakat 'eksenel vektör' olduğu için, görüntüde yön değiştirmemiş. Ama x ekseni yön değiştirdiğinden, işareti değişmiş. Buradaki can alıcı nokta, L ile H arasındaki bu davranış farkı...